🕹️OpenGL丨Object Mouse Trackball - 魔方作业(2)

Trackball原理

我们使用TrackBall来实现鼠标对于物体的自由旋转，我们在屏幕外虚构一个球形曲面，使鼠标在二维屏幕上的移动投影到球形曲面上，以实现更佳的用户体验。

The motivation behind the trackball (aka arcball) is to provide an intuitive user interface for complex 3D object rotation via a simple, virtual sphere - the screen space analogy to the familiar input device bearing the same name.

The sphere is a good choice for a virtual trackball because it makes a good enclosure for most any object; and its surface is smooth and continuous, which is important in the generation of smooth rotations in response to smooth mouse movements. Any smooth, continuous shape, however, could be used, so long as points on its surface can be generated in a consistent way.

假设我们的虚拟球面为 x^2+y^2+z^2=1 ，即以屏幕中心为球心，半径为1的球。将屏幕坐标映射到(-1,1)，由于映射点具有相同的x,y坐标，我们通过球面方程得到映射后的点坐标；若点在球面外，我们暂定映射到球面边缘的点。 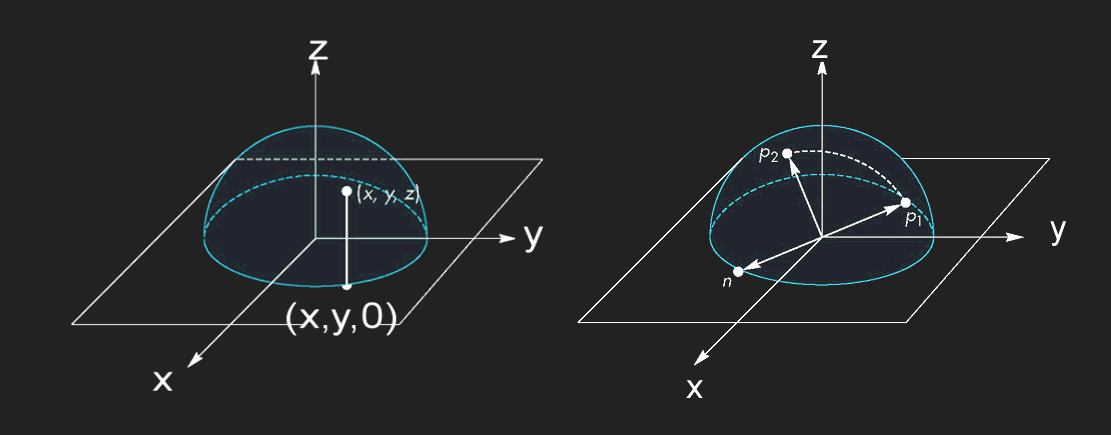当鼠标从P1移动到P2时，我们就可以通过叉乘计算旋转的轴与角度了。

开整

首先我们需要监听鼠标的按钮事件，我们使用glfw提供的回调函数接口，并启用对鼠标的输入监听。

    glfwSetMouseButtonCallback(window, click_callback);
...
    // tell GLFW to capture our mouse
    glfwSetInputMode(window, GLFW_CURSOR, GLFW_CURSOR_NORMAL);

glfwSetInputMode的第三个参数有三个模式：GLFW_CURSOR_NORMAL，GLFW_CURSOR_HIDDEN 和 GLFW_CURSOR_DISABLE；在DISABLE时可以虚拟和无限的光标移动，我们之前的FPS camera就是用的这个模式。

参考rubikcube的框架，我们使用两个bool值记录左键和右键的状态，今天我们先只处理左键的部分。

void click_callback(GLFWwindow* window, int button, int action, int mods) {
    if (button == GLFW_MOUSE_BUTTON_1) {
        if (action == GLFW_RELEASE) {
            leftkey = false;
            rightkey = false;
            return;
        }
        leftkey = true;
        rightkey = false;
        double keyx, keyy;
        glfwGetCursorPos(window, &keyx, &keyy);
        //std::cout << keyx << ',' << keyy << std::endl;
        //remap screenpos to [-1,1]
        trackball.mouseClick(glm::vec2(keyx / SCR_WIDTH, keyy / SCR_HEIGHT) * 2.0f - 1.0f);
     }
}

当鼠标点击时，我们调用mouseClick()事件，把鼠标位置投影到球面并存储到lastPos中：

void TrackBall::mouseClick(glm::vec2 pos2D) {
    mapToSphere(pos2D, lastpos);
}

void TrackBall::mapToSphere(const glm::vec2 pos2D, glm::vec3& pos3D) {
    //pos2D had been remapped to (-1,1) and our sphere is x^2+y^2+z^2=1.
    float d = pos2D.length();
    if (d < 1.0f)
        pos3D = glm::vec3(pos2D, sqrt(1 - d * d));
    else
        //if the point is outside the circle,project it to the nearest point on the circle.
        pos3D = glm::vec3(glm::normalize(pos2D), 0.0f);
}

通过记录点击状态的布尔值，我们调用mouseMove()函数计算转动：

// glfw: whenever the mouse moves, this callback is called
// -------------------------------------------------------
void mouse_callback(GLFWwindow* window, double xposIn, double yposIn)
{
    float keyx = static_cast<float>(xposIn);
    float keyy = static_cast<float>(yposIn);
    if (leftkey) {
        trackball.mouseMove(glm::vec2(keyx / SCR_WIDTH, keyy / SCR_HEIGHT) * 2.0f - 1.0f);
    }
}
void TrackBall::mouseMove(glm::vec2 pos2D) {
    glm::vec3 curpos = glm::vec3(0.0f);
    mapToSphere(pos2D, curpos);
    glm::vec3 axis = glm::cross(lastpos, curpos);
    float angle =  glm::length(lastpos - curpos);
    matrix = glm::rotate(matrix, angle, axis);
    lastpos = curpos;
}

好像看起来挺正确的！......耶？

debug！

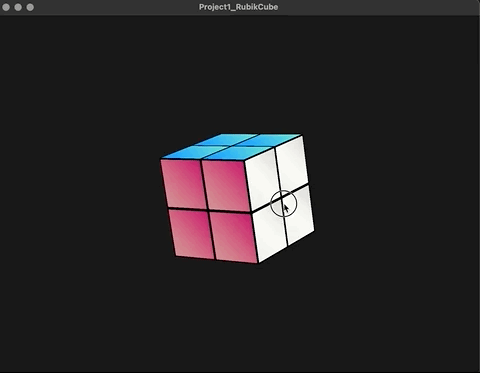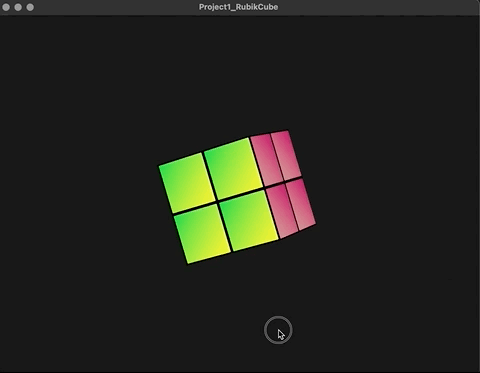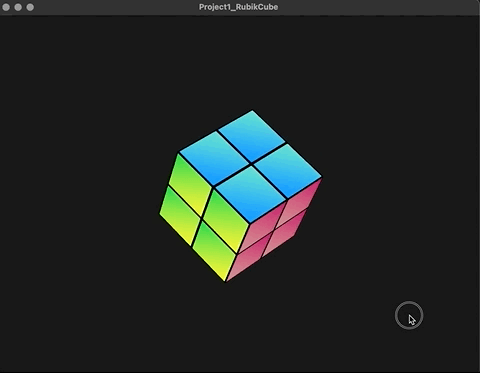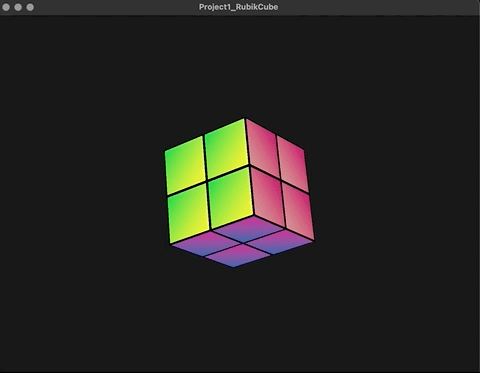
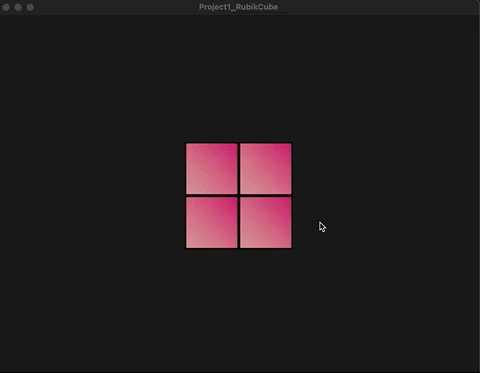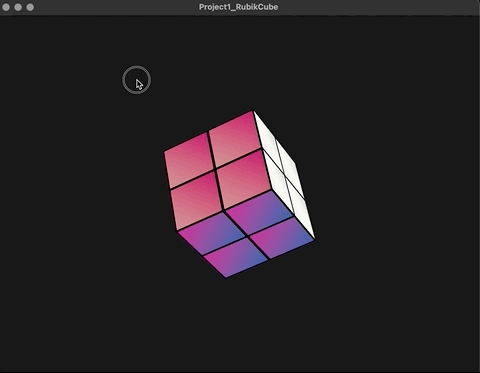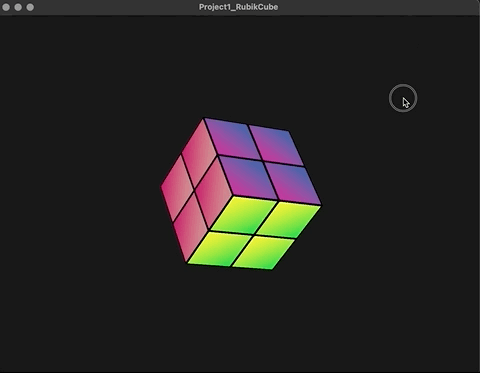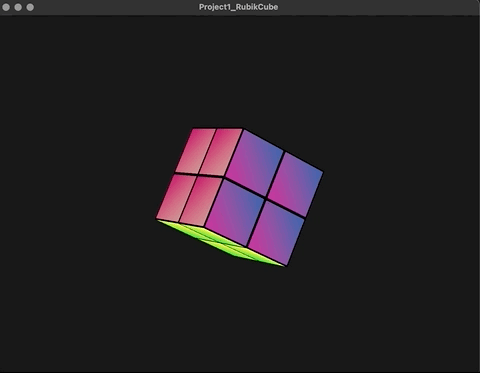
在原先的构思上，整个魔方旋转的矩阵是作为Model->World的坐标转换乘进去的，但是现状显然不是。观察上图，蓝色面为模型空间的上方向，后续本来应该沿世界坐标空间的y轴转动其实是在沿物体坐标空间的y轴转动。 emmmm..........

void TrackBall::mouseMove(glm::vec2 pos2D) {
    glm::vec3 curpos = glm::vec3(0.0f);
    mapToSphere(pos2D, curpos);
    glm::vec3 axis_w = glm::cross(lastpos, curpos);
    glm::vec3 axis_l = glm::vec3(glm::inverse(matrix) * glm::vec4(axis_w, 1));
    float angle =  glm::length(lastpos - curpos);
    matrix = glm::rotate(matrix, angle, axis_l);
    lastpos = curpos;
}

大概解决了一半！转动搞定了，但不知道为啥还是会突然消失。有可能是角度一直累加？可能需要换四元数之类的？ 周一问问助教再回来update。

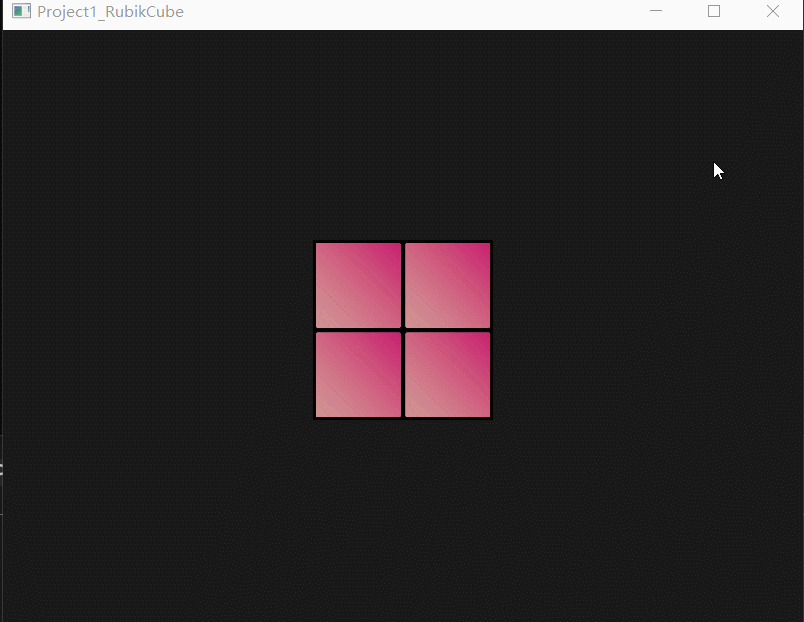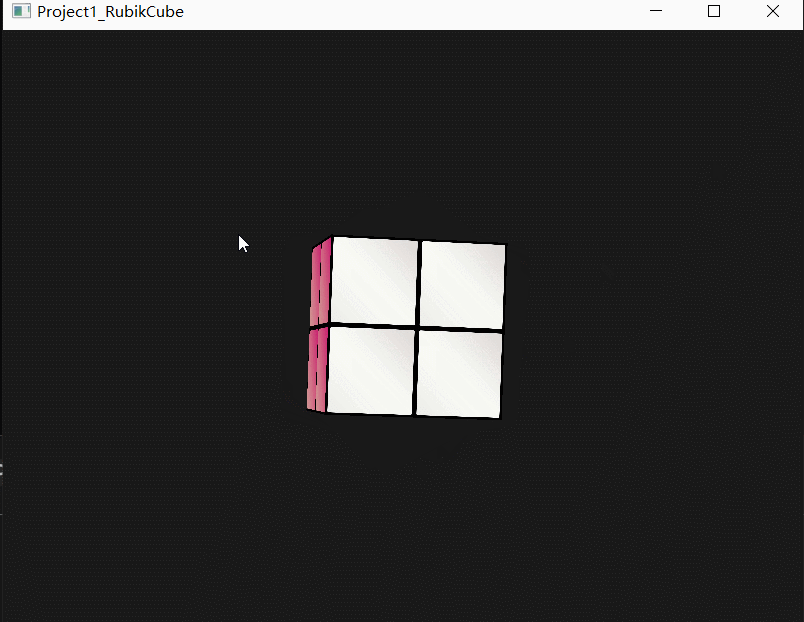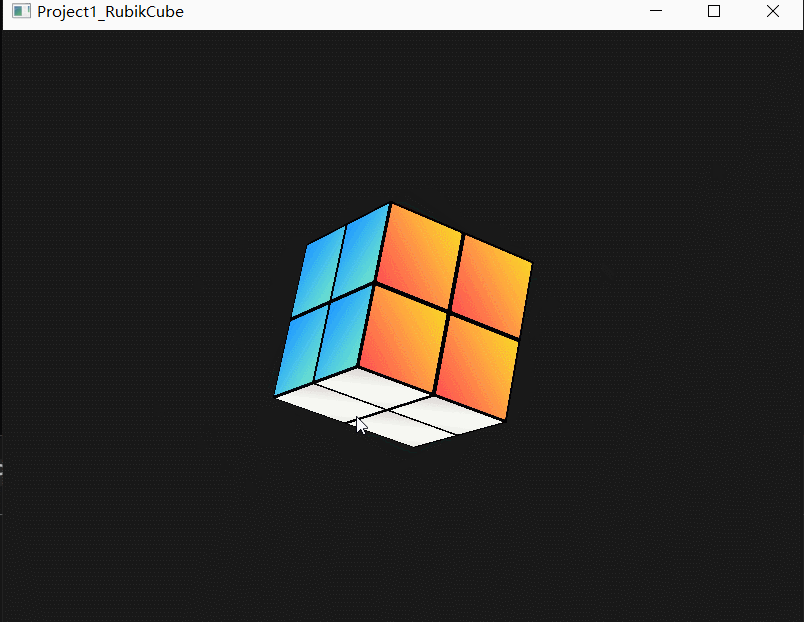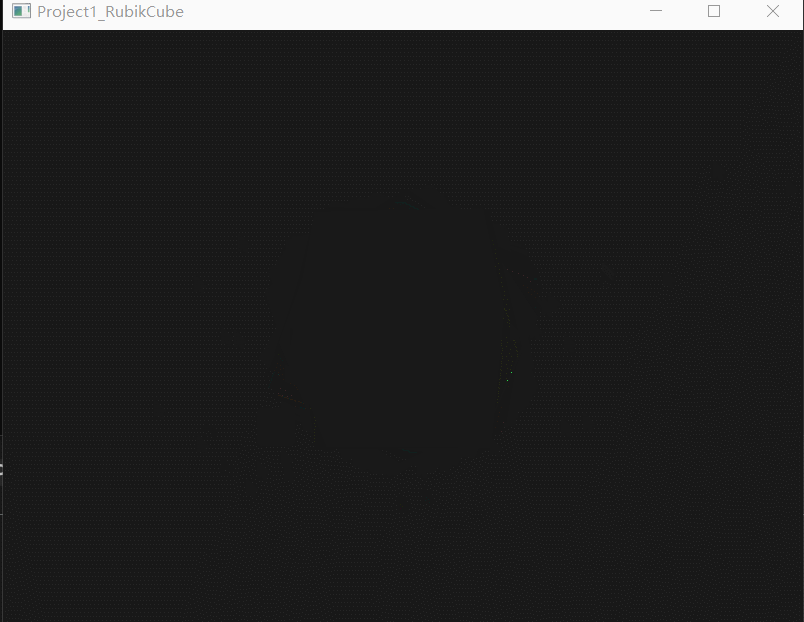
*** 已解决，虽然不知道原因是什么....详见🕹️OpenGL丨魔方最终版！ - 魔方作业(5)

更柔和的转动

让我们回来关注一下落在圆外的点，之前的策略是直接映射到圆最近的点上；wiki中给出了一个更平滑的拟合方法：使用一个喇叭形的双曲线曲面与球面拼合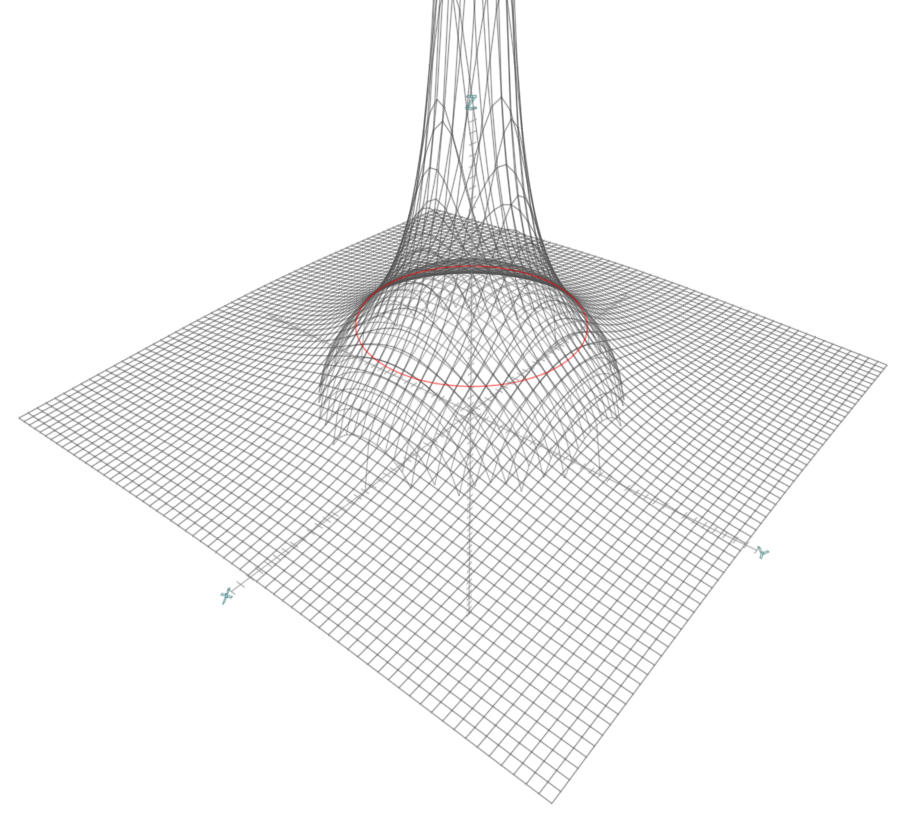： 其交线圆的方程为x^2 + y^2 = r^2 / 2，对于我们半径1的圆而言，交界点就是√2/2啦。

void TrackBall::mapToSphere(glm::vec2 pos2D, glm::vec3& pos3D) {
    //pos2D had been remapped to (-1,1)
    //sphere + hyperbolic sheet
    static const float sqrt2 = sqrt(2.0f);
    float d = glm::length(pos2D);
    if (d < sqrt2/2.f)
        //inside shpere
        pos3D = glm::vec3(pos2D, sqrt(1 - d * d));
    else 
        pos3D = glm::vec3(pos2D, 0.5f/d);
    pos3D = glm::normalize(pos3D);
}

即时δ还是δ累加？

TrackBall的轴与角度都是通过至少两个位置得出的，即当前位置&先前位置。上文中，我们的先前位置是[上一帧]的鼠标位置，即像是求δtime一样每次计算后就用curPos更新lastPos，因此TrackBall的转动是不断累加于matrix矩阵上的。 换个思路，我们的先前位置也可以考虑使用[第一帧]的鼠标位置，由于鼠标变化是(差不多)连续的，理论上我们与第一帧去计算得到的轴与旋转角也是(差不多)连续的。

void TrackBall::mouseMove(glm::vec2 pos2D) {
    glm::vec3 curpos = glm::vec3(0.0f);
    mapToSphere(pos2D, curpos);
    glm::vec3 axis_w = glm::cross(lastpos, curpos);
    glm::vec3 axis_l = glm::vec3(glm::inverse(matrix) * glm::vec4(axis_w, 1));
    float angle =  glm::length(lastpos - curpos);

        glm::mat4 r = glm::mat4(1.0f);
        matrix = glm::rotate(r,angle,axis_l);
}

使用即时δ的转动效果会感觉对鼠标的追踪更加准确，但旋转的过程不如δ累加连续，尤其是当鼠标靠近TrackBall边缘时，会有一些不自然的扭动。大家可以按需选择~

（对比一下之前的效果，我会更喜欢累加的计算结果呢）

在我的魔方项目中，左键对整体魔方的旋转是使用的δ累加的方式，而右键对魔方某一层的旋转是使用的即时δ的方式。

by ERIN.Z