#️⃣ Python | 基于taichi的WCSPH流体模拟

by ERIN.Z, 2022-11-27

终于交作业了！！！零python经验看不懂ppt上的各种公式万分痛苦地肝了两个星期。虽然只完成了基础分最低的算法... 没精力再单独写博客了，直接贴一下提交的文档吧。

1.程序概述

1.1 概述

程序基于拉格朗日视角，实现了基于WCSPH算法的三维流体模拟，演示了流体柱塌缩坠落并冲击容器的场景。

(效果图中mesh表面构建与平滑于Houdini中完成)

1.2 依赖库

taichi v1.2.2

( python 3.10 )

1.3 WCSPH算法

WCSPH(weakly compressible sph)算法属于SPH的显式求解算法，基于连续性方程、动量方程和状态方程，直接计算作用在各个颗粒上的压力、体力、粘聚力和表面张力的合力，继而求出加速度进而结合边界条件进行速度位置的更新。

WCSPH将液体密度视为一个变量，随粒子于每个状态更新。解算时每一帧的基本过程如下：

1.初始化粒子，为邻域搜索做准备；

2.计算粒子密度；

3.计算重力、压力、粘聚力、表面张力，根据加速度a更新粒子的速度v、位置x；

4.粒子可视化

2.程序结构

2.1 GLOBAL SETTINGS

模拟的宏观控制变量，包括taichi初始化(ti.init()),边界尺寸(Boundary), 流体尺寸(fluid), 粒子半径(particle_r), 输出控制(output)。

⚠: 默认taichi使用cuda构建。由于邻域搜索使用了taichi.algorithms.PrefixSumExecutor 并行求解前缀和，可能不支持部分类型的taichi构建。

2.2 PARTICLE PROPERTIES

粒子相关属性及储存空间。

常量

particle_2r 粒子直径

particle_h support radius，默认取值为4*particle_r

particle_V 粒子体积，球体体积近似值

particle_m 粒子质量，默认以水密度(1000)计算

particle_num 粒子数量

grid_size 网格边长，默认取值为particle_h

grid_num 网格数量

变量与场

particle_x 三维向量场 - 粒子位置

particle_v 三维向量场 - 粒子速度

particle_a 三维向量场 - 粒子加速度

particle_d 标量场 - 粒子密度

particle_p 标量场 - 粒子压强

particle_grid 三维向量场 - 粒子所在格id （用于邻域搜索）

由于邻域搜索时对粒子进行了再排序，这里还创建了x_buffer v_buffer grid_buffer grid_sort 等场。详见3.1节邻域搜索实现。

邻域搜索相关

grid_particles_num 标量场，每格粒子数

prefix_sum_executor 前缀和计算器，详见3.1节邻域搜索实现。

2.3 PARTICLE FUNCTIONS

粒子初始化与重排序的相关方法。

粒子初始化

init_fluid()

Func：根据fluid生成粒子坐标，并添加粒子；开始模拟前执行一次。

@ti.kernel add_particles(pos: ti.types.ndarray())

Input: init_fluid()计算的位置坐标序列；

Func: 并行初始化粒子初始状态；

网格初始化

init_grid_system()

Func: 初始化网格系统；模拟的每帧计算前执行。包含以下三步：

@ti.kernel update_grid_id()

Func: 计算每个粒子所在格，更新particle_grid与grid_particles_num。
@ti.kernel PrefixSumExecutor.run(input_arr)

Func: 于原位计算grid_particles_num前缀和。

@ti.kernel rearrange_by_grid()

Func: 按照格顺序重新排列particle_x/v/a等粒子信息。

@ti.Func pos_to_index(pos)

Func: 由三维坐标计算三维的网格索引(grid_index)

@ti.Func flatten_grid_index(grid_index)

Func: 由三维的网格索引计算一维的网格id(grid_id，即grid_particles_num的序列索引值)

2.4 SPH PROPERTIES

SPH相关属性。

基础物理值

SPH_dt 迭代步长

SPH_g 重力加速度

SPH_viscosity 粘滞力系数

SPH_sur_tension 表面张力系数

SPH_d_0 参照密度，默认为水密度(1000).

WCSPH

WCSPH的压力求解公式为：

p=k_{Eos}((\frac{\rho}{\rho _0})^\gamma-1)

SPH_stiffness 压力公式中参数 k_{Eos}

SPH_exponent 压力公式中参数 \gamma

SPH_collision_loss 粒子触壁反弹的速度损失

2.5 SPH FUNCTIONS

核函数

为保证导数的连续性，选用Cubic Spline Kernel（Monaghen 1992）.

W(r,h) = \sigma_d \begin{cases} 6(q^3-q^2)+1 & \text{for}\ 0\leq q\leq \frac{1}{2}\\ 2(1-q)^3 & \text{for}\ \frac{1}{2}<q\leq 1 \\ 0 & \text{otherwise} \end{cases}\\ \text{with}\ q= \frac{1}{h}||r||

其中 \sigma_d 是dimensional normalizing factor :

\sigma_3=\begin{cases} \frac{2}{3h},\quad&\rm{for\dim=1}\\ \frac{10}{7\pi h^2},&\rm{for\dim=2}\\ \frac{1}{\pi h^3},&\rm{for\dim=3}\ \end{cases}

@ti.func cubix_kernel(r)

Func: 计算核函数

@ti.func cubic_kernel_derivative(r)

Func: 计算核函数梯度

密度计算

WCSPH中压力的计算基于密度采样，因此首先对密度进行计算：

\rho_i = \sum_{j=0}^{n}\rho _jW(r_j-r_j,h)= \sum_{j=0}^{n}m_jW_{ij}

@ti.kernel compute_densities()

Func: 计算粒子密度

加速度计算

根据N-S方程:

\rho\frac{Dv}{Dt} = \rho g -\nabla p + \mu\nabla^2v

分别求解各部分力，与这些力贡献的加速度。

- 非压力项

重力

默认为重力加速度g：

@ti.kernel compute_gravity()

Func: 计算重力加速度。

粘滞力

使用了人工的粘滞阻力(artificial viscosity)。粘滞力的Anti-Symmetric Form计算公式为：

\mu\nabla^2v_i = \mu\sum_{j=0}^n m_j\frac{v_j-v_i}{\rho _j}\nabla^2W_{ij}

实际模拟中使用了标准形式的近似（Monaghan 2005），将二阶的\nabla ^2转化为一阶的\nabla：

\mu \nabla ^2v_i = \mu2(d+2)\sum_{j=0}^n\frac{m_j}{\rho_j}(\frac{v_{ij}·x_{ij}}{||x_{ij}||^2+0.01h^2})\nabla W_{ij}

@ti.kernel compute_viscosity()

Func: 计算粘滞力加速度。

表面张力

表面张力的求解参考了Becker 2007的方法：

\frac{d\mathbf{v}_i}{dt}=-\frac{\kappa}{m_i}\sum_jm_j(x_i-x_j)W_{ij}

@ti.kernel compute_sur_tension()

Func: 计算表面张力的加速度。

- 压力项

对于WCSPH，其压力求解其实类似于理想气体方程(EOS) :p=\rho RT, WCSPH中表示为：

p=k_{Eos}((\frac{\rho}{\rho _0})^\gamma-1)

由于气液边界采样时粒子不足，\rho_i 可能小于\rho_0 ,为气液边界不会产生向外的压力，这里带入公式的密度为：

\rho_i =max(\rho_i,\rho_0)

计算压强后即可求解压力贡献的加速度：

-\frac{1}{\rho_i}\nabla p_i =- \sum^n_{j=0}(\frac{p_i}{\rho _i^2}+\frac{p_j}{\rho_j^2})\nabla W_{ij}

@ki.kernel compute_pressure()

Func: 计算压强与压力产生的加速度。

显式积分

@ti.kernel advect()

Func: 辛欧拉法，用计算的加速度更新粒子速度，继而更新粒子位置。

边界条件

由于模拟的边界条件很简单，是与轴平行的正交平面，可直接通过坐标判断是否超出边界，对速度模拟计算触壁反弹。

@ti.kernel enforce_boundary()

Func: 更改粒子和速度，防止粒子超出边界。

Finally

WCSPH_step()

Func: 按照顺序包含上述解算步骤：

  init_grid_system()
  compute_densities()
  compute_gravity()
  compute_pressure()
  compute_viscosity()
  compute_sur_tension()
  advect()
  enforce_boundary()

2.6 DISPLAY PROPERTIES

可视化利用了taichi.GGUI系统，这部分设置了各类信息的显示颜色与边界可视化的顶点信息。

2.7 MAIN FUNCTION

主函数，主要步骤如下：

1.初始化流体粒子

2.初始化窗口

3.模拟计算

4.结果可视化

（5.输出.ply文件）

笔者硬件为NVIDIA RTX 2070, 若每迭代一次即绘制，约为155fps；为获得更符合现实的模拟效果，提交文件为每迭代10次后绘制一帧，约为20fps。

3.补充说明

3.1 操作说明

于GLOBAL SETTINGS代码块可修改边界尺寸/液柱尺寸。
运行run_simulation.py即可。

3.2 邻域搜索

邻域搜索的实现主要使用了grid系统。最初写二维WCSPH时，使用了链表搜索的数据结构（如下图）。

需定义每格最多的粒子数grid_max_particles,然后以此为长度开辟储存空间，保存每格的粒子序号；并以ti.root.X的方式构建数据间的链接关系（如下图，图源taichi doc）

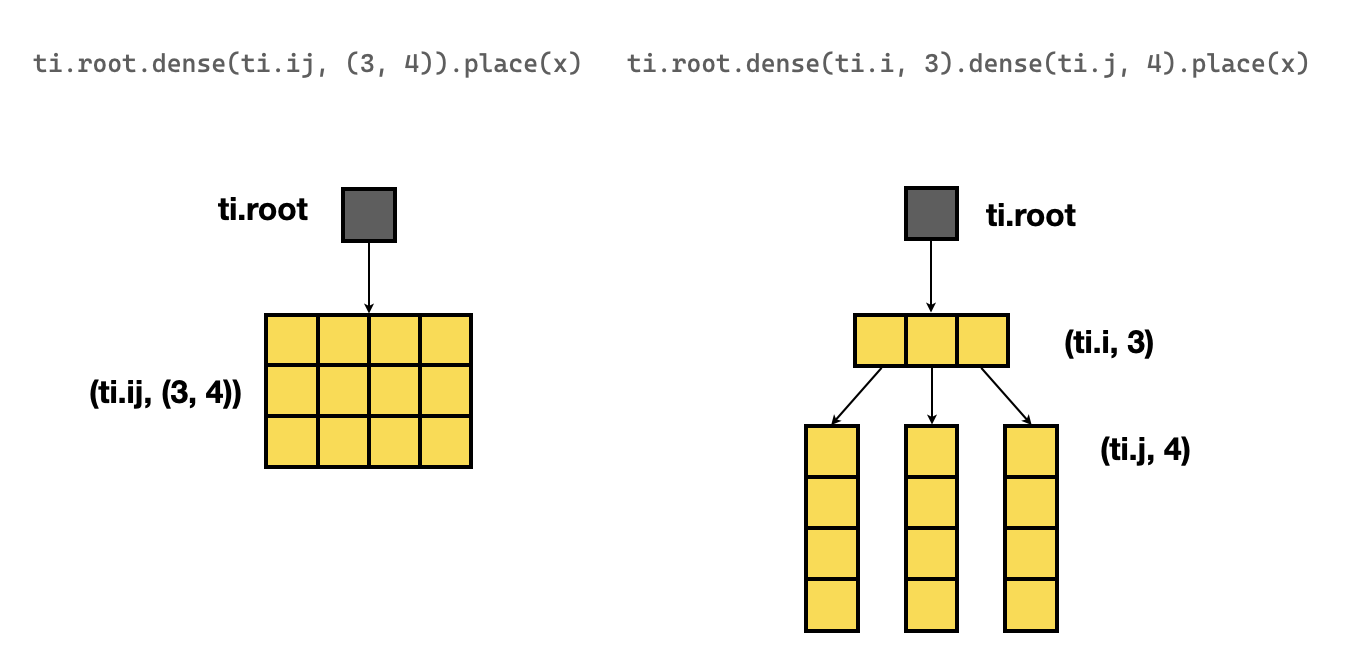
但从二维扩展至三维时，由于维度的增加，所需的内存空间陡增。但哪怕taichi.init()时，声明分配更多的内存空间给运算，依然存在内存分配失败的问题。最终卡了很久后，转为以排序时间为代价节省每格的存储空间。实现主要参考：https://github.com/erizmr/SPH_Taichi/blob/master/particle_system.py

邻域搜索主要维护了两个列表：每格粒子所在格particle_grid与每格的粒子数grid_particles_num；前者的索引顺序与其他的粒子属性相同，长度为粒子数；后者的索引顺序是扁平化的格id（由flatten_grid_id()得到）。（如下图，自绘）

注：为避免混淆，所有三维的格索引称为grid_index，如(0,0,0)；而一维的格索引称为grid_index, 如0.

在init_grid() 的过程中，首先会将grid_particles_num初始化为0，然后并行计算particle_grid,对对应格的grid_particles_num执行atomic_add().

其次计算前缀合，并根据grid的顺序，对所有particle参数重新排序，示例过程如下：（图源自绘）

重排序后，若想获取id为i的格内粒子，则以range(grid_particles_num[i-1],grid_particles_num[i])为索引序号查找粒子即可。（如下图，图源自绘）

3.3 可视化

由于笔者代码功底较弱，选择使用Houdini来进行模拟结果的可视化。

taichi可将点云信息输出为.ply文件，以便Houdini读取。在Houdini中进行了表面的重建、网格平滑与网格简化。示例mp4中每20步输出一帧点云信息，渲染后以60fps输出视频(因为帧渲多了...)

4.参考

4.1 参考文献

J. Monaghan, Smoothed Particle Hydrodynamics, “Annual Review of Astronomy and Astrophysics”, 30 (1992), pp. 543-574.
M. Becker and M. Teschner (2007). "Weakly compressible SPH for free surface flows". In:Proceedings of the 2007 ACM SIGGRAPH/Eurographics symposium on Computer animation. Eurographics Association, pp. 209–217.

4.2 参考代码与教程

太极图形课S1第十讲：流体仿真01
SPlisHSPlasH tutorials

by ERIN.Z