#️⃣ Python | 拉普拉斯网格变形

by ERIN.Z, 2022-12-04

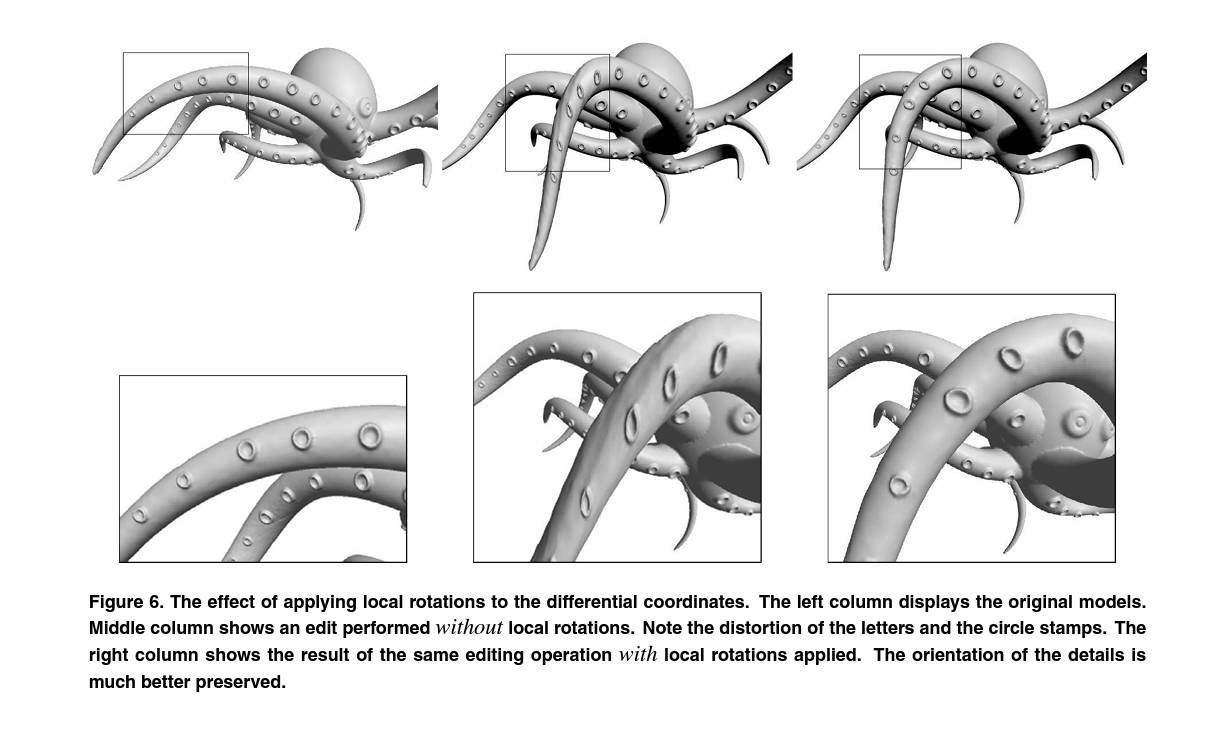
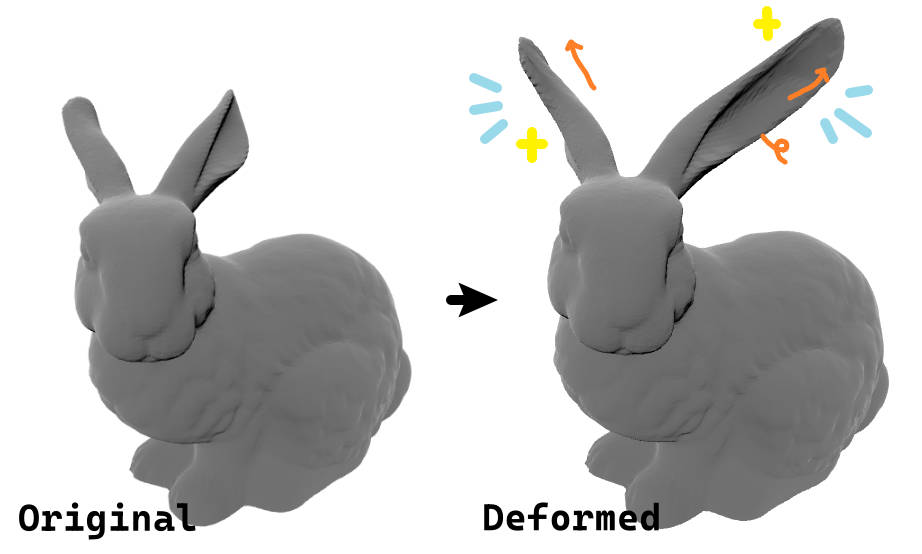
今天压ddl写完动画原理与算法的小作业，也是关于三维网格的题目。那么就先发出Mesh系列的第二篇——

（简化版）网格变形实操！

问题描述

拉普拉斯网格变形的基本思路是,对网格进行变形时(让控制点(anchor)在变形后处于目标位置)，保持网格内在结构(保证顶点的相对坐标发生的变化尽可能小)

顶点的相对坐标的定义:
\delta_i = \mathscr{L}\left(\mathbf{v}_{i}\right)=\mathbf{v}_{i}-\frac{1}{d_{i}} \sum_{j \in \mathbb{N}_{i}} \mathbf{v}_{j} \ , \quad i=1, \ldots,n

其中 \mathbf{v_i} 是顶点 i 的绝对坐标，\delta_i 是相对坐标，d_i 是顶点的度数，\mathbb{N}_i 是其邻域。
绝对坐标V与相对坐标\Delta之间的转换:
\Delta = (I - D^{-1}A)V = LV

其中 A 是 0-1 邻接矩阵，D 是度数矩阵, L = (I - D^{-1}A) 是谱图论中的拉普拉斯矩阵

预备知识补充时间：

微分坐标系 Differential Coordinates

题目中提到的“相对坐标”即微分坐标，定义为“该点的全局坐标减去所有邻居顶点全局坐标的平均值”。

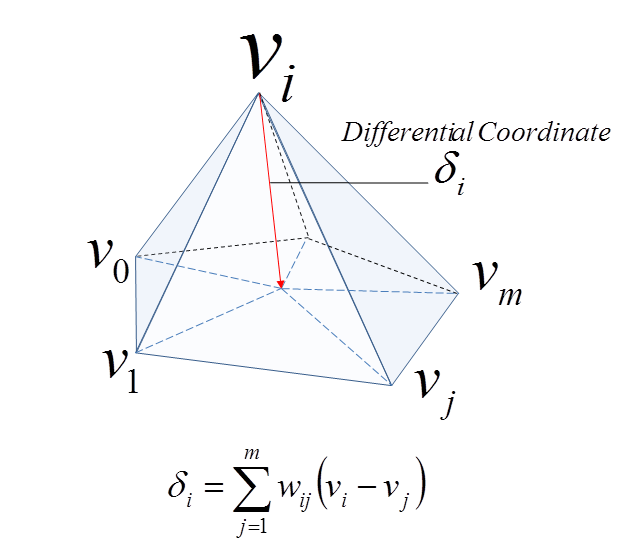
全局坐标和微分坐标之间的变换是线性的，因此可以表示为上文中的矩阵形式：

\Delta = (I - D^{-1}A)V = LV

其中V表示全局坐标，\Delta表示微分坐标，A表示邻接矩阵，D表示度数矩阵，二者可表示如下：

A_{ij}=\begin{cases} 1&&i\in N(i)\\ 0&&\text{otherwise} \end{cases} \\ D_{ij}=\begin{cases} d_j&&i=j\\ 0&&\text{otherwise} \end{cases}

L是图论中 拉普拉斯矩阵 的 RW规范化形式 . (...)

拉普拉斯矩阵 Laplacian Matrix

拉普拉斯矩阵，也称调和矩阵。主要应用在图论中，作为一个图的矩阵表示。它具有很多形式，最普通的拉普拉斯矩阵定义为L=D-A。常用的还有“对称规范化拉普拉斯矩阵 (Symmetric normalized Laplacian）”,L^{sym}

L^{sym}=D^{-\frac{1}{2}}LD^{-\frac{1}{2}}=I-D^{-\frac{1}{2}}AD^{-\frac{1}{2}}\\ \\ L^{sym}_{i,j} =\begin{cases} 1&&\text{if }i=j\text{ and }deg(v_i)\neq0\\ -\frac{1}{\sqrt{deg(v_i)deg(v_j)}}&&\text{if }i\neq j\text{ and }v_i\text{ is adjacent to }v_j\\ 0&&\text{otherwise.} \end{cases}

本文中用到的是“RW规范化拉普拉斯矩阵 (Random walk normalized Laplacian）”,L^{rw}

L^{rw}=D^{-1}L=I-D^{-1}A\\ \\ L^{rw}_{i,j} =\begin{cases} 1&&\text{if }i=j\text{ and }deg(v_i)\neq0\\ -\frac{1}{deg(v_i)}&&\text{if }i\neq j\text{ and }v_i\text{ is adjacent to }v_j\\ 0&&\text{otherwise.} \end{cases}

（打latex已经很熟练了....欣慰，感觉自己勉强达到了工科大学生大一水平）

微分坐标用于变形

微分坐标是一种内在的表示(Intrinsic surface representation),可以使得变形过程仍然保持局部细节，求解速度也很快。求解时满足两个条件：

Detail constraints： Lx = \delta
Modeling constraints: x_j = c_j, j\in {j_1,j_2,...,j_k} 具体矩阵的求解过程太多数学了不是特别理解..大体上我们需要在L$下方扩展k行（k为改变的锚点数），锚点所在点为1. 不过求解的框架老师已经给搭好了，我们就边读边理解吧~！

求解算法

输入

变形前绝对坐标 V
相对坐标 \Delta
控制点集合 P_\text{anchors}

输出

变形后绝对坐标 V'

目标

保持 V’ 相对坐标与输入相对坐标 \Delta 尽可能一致

\Delta - \mathscr{L}(V') \rightarrow 0

要让控制点在变形后处于目标位置

\mathbf{v}_{i}^{\prime}-\mathbf{u}_{i}=0 \ , \quad i \in P_\text{anchors}

实现

提示1: 采用最小二乘法求解；
提示2: 采用稀疏矩阵表示提高效率。

Code

在Jupyter Notebook环境下，作业使用Trimesh处理三维网格，用scipy.sparse处理稀疏矩阵。

# 导入必要的库
from trimesh import Scene
from mesh import TriMesh
import numpy as np
import io
from trimesh.viewer.notebook import scene_to_notebook
from scipy.sparse import coo_matrix
from scipy.sparse.linalg import lsqr
import matplotlib.pyplot as plt

get_LeastSquareMatrix()函数需要求的就是上图中左侧的那一大坨矩阵，也是本次小作业中要实现的部分：

# 目的: 定义目标方程的左手边矩阵(稀疏表示)
def get_LeastSquareMatrix(adjacent_mat, anchors_indices):
    # 输入: 三角网格的邻接矩阵表示, 控制点的索引
    n = len(adjacent_mat.keys()) # 节点数
    k = len(anchors_indices) # 控制点数
    I = [] # 稀疏矩阵的非零行
    J = [] # 稀疏矩阵的非零列
    V = [] # 稀疏矩阵的非零值

    # 任务一: 构建拉普拉斯稀疏矩阵
    for i in range(n):
        indices = adjacent_mat[i]
        z = len(indices)
        if(z!=0):
            I.append(i)
            J.append(i)
            V.append(1)
            for j in range(z):
                I.append(i)
                J.append(indices[j])
                V.append(-1.0/z)

    # 任务二: 行向下扩增K行 -- 控制点的约束默认最小二乘权重系数为1
    for i in range(k):
        anchor_idx = anchors_indices[i]
        I.append(n+i)
        J.append(anchor_idx)
        V.append(1)    

    #输出: ((n+k) x n 的稀疏矩阵, n是连接节点数, k是控制点数量
    L = coo_matrix((V, (I, J)), shape=(n + k, n)).tocsr()    
    return L

使用上述的左侧矩阵构成方程，用最小二乘求解。

# 目的: 最小二乘求解求解得到变形后的节点位置
# 该函数不用修改
def solve_Laplacian(adjacent_mat, vertices_pos, anchors_indices, anchors_pos):
    n = len(adjacent_mat.keys()) # 节点数
    k = len(anchors_indices) # 控制点数
    V_prime = np.zeros((n,3))    
    L = get_LeastSquareMatrix(adjacent_mat,anchors_indices) # 最小二乘矩阵
    delta =  np.array(L.dot(vertices_pos)) # 求解微分坐标
    for i in range(k):
        delta[n + i, :] =  anchors_pos[i, :]
    for i in range(3):
        V_prime[:, i] = lsqr(L, delta[:, i])[0] # 求解最小二乘
    return V_prime # 输出: 变形后的节点位置坐标

中间设置网格的代码省略一部分~实际求解的运用如下：

mesh = TriMesh("./meshes/bunny.ply") # 导入三角网格文件
ori_mesh = mesh.get_mesh_copy() 
scene_to_notebook(Scene([ori_mesh]))

...

adjacent_mat = mesh.get_neighbors() # 三角网格的邻接矩阵
vertices_pos = mesh.get_vertices() # 三角网格的节点坐标
############### 求解 Laplacian ############### 
V_prime = solve_Laplacian(adjacent_mat,vertices_pos, anchors_idx, anchors_pos)
new_mesh = mesh.update_vertices(V_prime,inplace=True)
scene_to_notebook(Scene([new_mesh]))

参考文献

O. Sorkine, D. Cohen-Or, Y. Lipman, M. Alexa, C. Rössl, H.-P. Seidel. Laplacian surface editing. SGP '04: Proceedings of the 2004 Eurographics/ACM SIGGRAPH symposium on Geometry processing. July 2004, Pages 175–184.

by ERIN.Z